티스토리 뷰
정렬이란?
컴퓨터 과학에서 정렬 알고리즘이란 원소들을 번호순이나 사전 순서와 같이 일정한 순서대로 열거하는 알고리즘입니다.
- 오름차순 정렬 : 1, 2, 3, ..., n-1, n
- 내림차순 정렬 : n, n-1 ... 3, 2, 1
알고리즘 복잡도 계산
정렬 알고리즘은 매우 다양하기 때문에 각각의 효율성을 비교하기 위해 알고리즘 복잡도를 계산합니다.
- 시간 복잡도 : 알고리즘 실행 속도 (시간 효율성)
- 공간 복잡도 : 알고리즘이 사용하는 메모리 사이즈 (메모리 공간 효율성)
이러한 시간/공간 복잡도를 나타내는 방법으로 빅오(Big-O), 빅오메가(Big-Ω), 빅세타(Big-Θ) 표기법이 있습니다.
빅오 표기법(big-O notation)이란?
빅오 표기법은 알고리즘의 효율성을 표기해주는 기법으로 상한선 기준(최악의 시간)의 시간복잡도를 나타냅니다.
입력 n에 따라 몇번 계산이 실행되는지를 표현식에 가장 큰 영향을 미치는 n의 단위로 표기하며 시간이 빠른순으로 나열하면 다음과 같습니다.
| O(1) < O(logn) < O(n) < O(nlogn) < O(n²) < O(2ⁿ) < O(n!) |

*빅오메가는 하한선 기준, 빅세타는 상한선과 하한선의 사이를 기준으로 표기함
대표적인 정렬 알고리즘
교환, 선택, 삽입 3가지 핵심요소를 통해 정렬하는 대표적인 알고리즘은 다음과 같습니다.
| Name | Best | Avg | Worst |
| 거품 정렬 (Bubble Sort) | O(n²) | O(n²) | O(n²) |
| 선택 정렬(Selection Sort) | O(n²) | O(n²) | O(n²) |
| 삽입 정렬(Insertion Sort) | O(n) | O(n²) | O(n²) |
| 퀵 정렬(Quick Sort) | O(nlogn) | O(nlogn) | O(n²) |
| 병합 정렬(Merge Sort) | O(nlogn) | O(nlogn) | O(nlogn) |
| 힙 정렬(Heap Sort) | O(nlogn) | O(nlogn) | O(nlogn) |
| 기수 정렬(Radix Sort) | O(n) | O(n) | O(n) |
| 계수 정렬(Counting Sort) | O(n) | O(n) | O(n) |
거품 정렬 (Bubble Sort)
버블 정렬은 서로 인접한 두 원소를 비교하여, 조건에 맞지 않다면 자리를 교환하며 정렬하는 알고리즘입니다.
(정렬 과정에서 원소의 이동이 거품이 수면으로 올라오는 듯한 모습을 보이기 때문에 버블정렬이라는 이름이 지어짐)
- 시간 복잡도 : O(n²)
- 공간 복잡도 : O(n)
- 장단점 : 구현이 쉽지만 비효율적
아래와 같이 0번 index부터 n-1번 index까지 n번까지의 모든 index를 비교하며 정렬합니다.

function bubbleSort (arr) {
for(let i = 0; i < arr.length; i++) {
for(let j = 0; j < arr.length -1 - i; j++) {
if(arr[j] > arr[j + 1]) {
let swap = arr[j]
arr[j] = arr[j + 1]
arr[j + 1] = swap
}
}
}
return arr
}
선택 정렬(Selection Sort)
선택 정렬은 해당 순서에 원소를 넣을 위치는 이미 정해져 있고, 어떤 원소를 넣을지 선택하는 알고리즘입니다.
- 시간 복잡도 : O(n²)
- 공간 복잡도 : O(n)
- 장단점 : 구현이 쉽지만 비효율적, 버블보다 약간 빠름
아래와 같이 첫 번째 값을 두 번째 부터 마지막 값까지 차례대로 비교하여 최솟값을 찾아 첫 번째에 놓고, 두 번째 값을 세 번째 부터 마지막 값까지 비교하여 최솟값을 찾아 두 번째 위치에 놓는 과정을 반복하며 정렬합니다.

function selectSort (arr) {
for(let i = 0; i < arr.length; i++) {
let min = i
for(let j = i + 1; j < arr.length; j++) {
if(arr[min] > arr[j]) {
min = j
}
}
if(min !== i) {
let swap = arr[min]
arr[min] = arr[i]
arr[i] = swap
}
}
return arr
}
삽입 정렬(Insertion Sort)
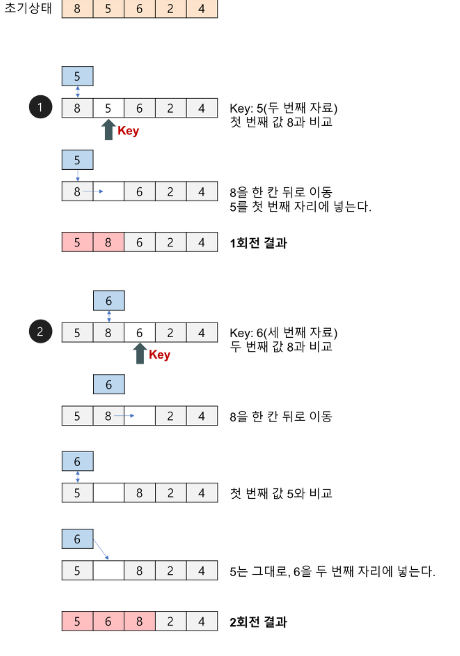
삽입 정렬은 두 번째 원소부터 시작하여 그 앞(왼쪽)의 원소들과 비교하여 삽입할 위치를 지정한 후, 원소를 뒤로 옮기고 지정된 자리에 자료를 삽입하여 정렬하는 알고리즘입니다.
- 시간 복잡도 : O(n) (최악의 경우 O(n²) )
- 공간 복잡도 : O(n)
- 장단점 : 성능이 좋아서 다른 정렬 알고리즘의 일부로 사용되기도 함, 데이터 상태나 크기에 따라 편차가 심함
function insertionSort(arr) {
for(let i = 1; i < arr.length; i ++) {
let cur = arr[i]
let left = i - 1
while(left >= 0) {
if(arr[left] > arr[left + 1]) {
arr[left + 1] = arr[left]
arr[left] = cur
}
left--
}
}
return arr
}
퀵 정렬(Quick Sort)
퀵 정렬은 분할 정복 방법을 통해 주어진 배열을 정렬합니다.
- 시간 복잡도 : O(nlogn) (최악의 경우 O(n²) )
- 공간 복잡도 : O(n)
- 장단점 : 매우 빠르지만 최악의 피봇을 선택할 경우 시간복잡도가 많이 늘어남
아래와 같이 피봇을 설정하고 피봇보다 큰 값과 작은 값으로 분할하여 정렬합니다. 병합 정렬과 달리 배열을 비균등하게 분할한다는 특징이 있습니다.

function quickSort(arr) {
if(arr.length <= 1) {
return arr
}
let cur = arr[0]
let left = []
let right = []
for(let i = 1; i < arr.length; i++) {
if(cur > arr[i]) {
left.push(arr[i])
} else {
right.push(arr[i])
}
}
let leftArr = quickSort(left)
let rightArr = quickSort(right)
return [...leftArr, cur, ...rightArr]
}
병합 정렬(Merge Sort)
병합 정렬은 합병 정렬이라고도 부르며, 분할/정복 방법을 통해 구현합니다.
- 시간 복잡도 : O(nlogn)
- 공간 복잡도 : O(n)
- 장단점 : 퀵 정렬과 달리 피봇을 설정하지 않아 기복이 없음, 추가적인 메모리가 필요하는 단점이 있음
아래와 같이 주어진 배열을 크기가 1인 배열로 분할하고 합병하면서 정렬을 진행하는 분할/정복 알고리즘입니다.

private void solve() {
int[] array = { 230, 10, 60, 550, 40, 220, 20 };
mergeSort(array, 0, array.length - 1);
for (int v : array) {
System.out.println(v);
}
}
public static void mergeSort(int[] array, int left, int right) {
if (left < right) {
int mid = (left + right) / 2;
mergeSort(array, left, mid);
mergeSort(array, mid + 1, right);
merge(array, left, mid, right);
}
}
public static void merge(int[] array, int left, int mid, int right) {
int[] L = Arrays.copyOfRange(array, left, mid + 1);
int[] R = Arrays.copyOfRange(array, mid + 1, right + 1);
int i = 0, j = 0, k = left;
int ll = L.length, rl = R.length;
while (i < ll && j < rl) {
if (L[i] <= R[j]) {
array[k] = L[i++];
} else {
array[k] = R[j++];
}
k++;
}
while (i < ll) {
array[k++] = L[i++];
}
while (j < rl) {
array[k++] = R[j++];
}
}
힙 정렬(Heap Sort)
힙 정렬은 *완전 이진 트리를 기본으로 하는 힙 자료구조를 기반으로 정렬하는 방식입니다.
- 시간 복잡도 : O(nlogn)
- 공간 복잡도 : O(n)
- 장단점 : 추가적인 메머리를 필요로 하지 않음, 데이터 상태에 비해 다른 정렬보다 느린 경우가 있음
*완전 이진 트리 : 삽입할 때 왼쪽부터 차례대로 추가하는 이진 트리
아래와 같이 주어진 데이터를 힙 자료구조로 만들어 최댓값 또는 최솟값부터 하나씩 꺼내서 정렬하는 알고리즘입니다.

private void solve() {
int[] array = { 230, 10, 60, 550, 40, 220, 20 };
heapSort(array);
for (int v : array) {
System.out.println(v);
}
}
public static void heapify(int array[], int n, int i) {
int p = i;
int l = i * 2 + 1;
int r = i * 2 + 2;
if (l < n && array[p] < array[l]) {
p = l;
}
if (r < n && array[p] < array[r]) {
p = r;
}
if (i != p) {
swap(array, p, i);
heapify(array, n, p);
}
}
public static void heapSort(int[] array) {
int n = array.length;
// init, max heap
for (int i = n / 2 - 1; i >= 0; i--) {
heapify(array, n, i);
}
// for extract max element from heap
for (int i = n - 1; i > 0; i--) {
swap(array, 0, i);
heapify(array, i, 0);
}
}
public static void swap(int[] array, int a, int b) {
int temp = array[a];
array[a] = array[b];
array[b] = temp;
}[참고]
https://ko.wikipedia.org/wiki/%EC%A0%95%EB%A0%AC_%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98
정렬 알고리즘 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 컴퓨터 과학과 수학에서 정렬 알고리즘(sorting algorithm)이란 원소들을 번호순이나 사전 순서와 같이 일정한 순서대로 열거하는 알고리즘이다. 효율적인 정렬은
ko.wikipedia.org
https://velog.io/@msriver/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-%EC%A0%95%EB%A0%AC%EC%9D%B4%EB%9E%80
[알고리즘] 정렬이란?
엑셀이나 문서작성 프로그램을 사용한 사람이라면 데이터를 오름차순 혹은 내림차순으로 정렬 해본적이 있을 것이다. 정렬이란 데이터의 집합을 어떠한 기준(핵심항목, key)의 대소관계를 따져
velog.io
javascript 정렬 알고리즘 종합 정리
배열 요소의 값 정리를 위한 알고리즘
velog.io
Big-O Notation 복잡도 - 정렬
알고리즘 복잡도 계산 항목1\. 시간 복잡도: 알고리즘 실행 속도2\. 공간 복잡도: 알고리즘이 사용하는 메모리 사이즈시간이 중요하다.알고리즘 최악의 실행 시간을 표기한다. (최소 이 성능을 보
velog.io
https://noahlogs.tistory.com/27
빅오 표기법 (big-O notation) 이란
컴퓨터 과학(Computer Science) 에서 알고리즘은 어떠한 문제를 해결하기 위한 방법이고, 어떠한 문제를 해결 하기 위한 방법은 다양하기 때문에 방법(알고리즘) 간에 효율성을 비교하기 위해 빅오(
noahlogs.tistory.com
정렬 알고리즘 정리
버블 정렬, 합병 정렬, 퀵 정렬
wooder2050.medium.com
👨🏻💻 Tech Interview
최종 수정 : 9/20/2022, 10:14:18 AM
gyoogle.dev
'CS > Algorithm' 카테고리의 다른 글
| [알고리즘] DP(Dynamic Programming)란? (0) | 2022.10.25 |
|---|---|
| [알고리즘] 에라토스테네스의 체 (0) | 2022.08.01 |
- Total
- Today
- Yesterday
- 자바
- 백준 node.js
- 자바스크립트
- fp
- 함수형 프로그래밍
- 렉시컬 환경
- 백준 javascript
- 객체지향 프로그래밍
- 비동기
- 2019 카카오 개발자 겨울 인턴
- 프로퍼티
- 프로그래머스
- 전역 변수
- 이분탐색
- JavaScript
- 모던 자바스크립트 deep dive
- git
- 디자인 패턴
- 운영체제
- 네트워크
- 다이나믹 프로그래밍
- 투포인터
- 프로토콜
- Baekjoon
- TDD
- 백준
- 카카오 인턴
- 알고리즘
- map
- 코딩테스트
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
